Risk-based method to determine inspections and inspection frequency

Extending inspection periods can result in a lower level of safety, but based on insight from using a mathematical model it is possible to use improvements to the rolling stock to create more efficient inspection schedules while maintaining the same level of safety.

Until recently, the trains of the Dutch Railways were inspected daily. Frequency and scope of inspections were prescribed by legislation and regulations. Inspections were designed to ensure that the rolling stock to be deployed for passenger service was placed with a sufficient degree of safety.

The new regulatory framework is much more functional and now prescribes that the train operating company (TOC) must ensure the safe use of the rolling stock. The requirement on the TOC to deploy trains safely creates the possibility for inspections to be more focussed and scheduled more efficiently.

To achieve a more efficient inspection schedule, the question was whether frequency and content of the inspections could be reduced using a risk-based approach. To be able to ensure safe deployment the ‘stand still’ principle is formulated as well as sufficient measures to prevent any casualties (the so called ALARP principle).

To determine a new inspection schedule and to be able to prove that it is satisfactory, it is necessary to know how the risks change in relation to the inspection frequency. A mathematical model was developed for this purpose.

Mathematical model for risk

The risk model describes the relationship between the inspection schedule and the total associated risk. The model has two parts:

• The rolling stock failure model. This part establishes the frequency of failure per type of failure of the rolling stock as a function of the inspection periods.
• The casualty model. This part lays a relationship between a certain type of failure, per period, of the rolling stock and the average number of FWSIs1 per period.

The total risk model consists of multiple rolling stock failure models and multiple casualty models. This represents the various ways of unsafe failure of the rolling stock.

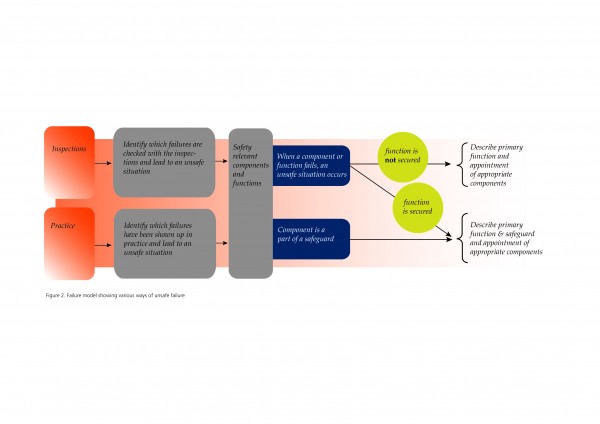
Failure model showing various ways of unsafe failure

Possible failures

For the analysis of all possible failure types, an existing installation with a given inspection schedule was assumed. Based on these inspections it is possible to indicate which components or functions are being inspected and are therefore relevant to safety. By considering this set of failure types one is considering that part of the risk that is currently covered by inspections. By using a risk-based management approach, all malfunctions of a dangerous nature were considered too. Therefore, all failures that can be realistically expected have been covered.

Inspected components or functions can upon failure lead to an unsafe situation and be part of a safeguard that must detect failure of the rolling stock or take over the function.

Functions that, upon failure, can result in an unsafe situation must be examined to see if there is a safeguard in place for them. If so, it must be examined to determine which function is safeguarded and what it does.

Functions can also be redundantly implemented. This must be included in the description of the failure type.

The failure model uses reliability data. In some functions, human failure is also a determining factor for the final risk.

Failure model

Reliability Centred Maintenance (RCM) describes how a relation can be found between the frequency of failure, the frequency of inspections and the reliability of the components in the installations.

The structure of the installation determines this relationship. In (RCM, 1997) the relationship was made between a function that is unsafe if it fails and that has a safeguard in place. Other types of systems had to be described.

Casualty model

The failure types of the rolling stock that could possibly result in FWSI are examined. For each failure an assessment is made of whether one or more FWSIs could occur. Moreover, a failure will not always result in a FWSI – for example, if the brakes fail. There are multiple boundary conditions that would need to be present before the failure leads to an FWSI. The combination of both mechanisms form the casualty model.

Mathematical model costs/risks

The risk for an FWSI generally decreases with more frequent inspections. More frequent inspections represent higher costs.

The costs of a single inspection depend on the duration and rate. With the number of inspections per period, the costs of the inspections can be calculated. The relation between inspection period and risk could be calculated with the same model as described before.

The extra costs to avoid an extra FWSI can be calculated per failure type using a numerical approximation.

Determining a new inspection schedule

Inspections are intended to reduce the risk. When creating the mathematical model, the inspections that influence the risk were determined. Which inspections affect the risk depends on the failure type. Depending on the installation, structure inspections affect the risk.

The new inspection schedule must satisfy the so-called ‘stand still’ principle. This means that the risk may not increase. The current risk can be determined by using the mathematical model with the inspection periods equal to the current periods.

At first it appears that extending the inspection period based on the ‘stand still’ principle is not possible. Increasing the inspection period results in an increase in risk (barring exceptions). There are three situations that allow lowering the inspection frequency:

• In the new situation, the rolling stock has become more reliable for other reasons
• Certain inspections do not impact the risk
• By carrying out more inspections for high risk and less inspections for low risk, a more optimal inspection schedule can be drawn up.

Using new reliability figures of components and new inspection periods mean the new risk can be determined.

An inspection period equal to the running maintenance cycle has been initially implemented. In the case that risk in the new situation is higher than in the current situation, the inspection interval must be shortened.

If the ALARP principle is complied with it must be evaluated per failure type. Per failure type that doesn’t comply with the ALARP condition means the inspection period must be shortened (or the installation modified).

Conclusion

A risk model that describes the relationship between inspection periods and risks clarifies:

• How the risks are related to each other
• That many risks hardly increase with an extended inspection period
• How improvements to the reliability of a component result in a reduction of the risk
• How the reduction of the risk from the previous point can be used to carry out less inspections while the total risk does not increase.

Using these methods, it is possible to derive a number representing risk. This makes it possible to compare various inspection schedules and determine whether they comply with a ‘stand still’ requirement and if sufficient provision has been made to avoid casualties.

Epilogue

The possibility of including this method in existing RBM software packages has been investigated. It would be a good addition to such programmes to include this part (or at least a link to it).

The same modelling can also be used to lay a relation between inspections and for example costs caused by a non-working installation. This method can therefore be applied to many more areas than just safety.

About the Author

Johan van der Werf

Johan van der Werf is Senior Consultant with Lloyd’s Register Rail in Utrecht, specialising in Sustainability/Energy Reduction process developments in the rail environment. Johan has 10 years experience in the rail industry as Technical Leader and Project Leader in the development of Electric Drives for Dutch Railways (NS). His background is Power Electronics and Drive and Control systems.